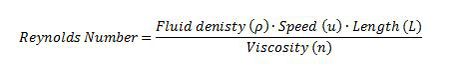Biophysics of Cell Motility
Introduction
By Dhruv Kumar Vig
Overview of Cell Motility
Cells are the primary building blocks of all living organisms and at a basic level their functions consist of growing, replicating, and dividing (Wolgemuth 2011). In order for a cell to complete these functions, they must produce force (Wolgemuth 2011). This force is produced by molecular motors that exist in the cell for example, in our muscles, myosin binds to actin filaments, thereby exerting forces (Wolgemuth 2011). These types of forces are able to be modeled using Brownian motion; however, this kind of modeling fails to address the molecular binding energies that are used by these molecules (Wolgemuth 2011). For instance, the binding and hydrolysis of ATP to a molecule completes a cycle of rotation that generates force; therefore, these molecules can be viewed as motors which can then be described by their force velocity relationship (Wolgemuth 2011). These forces also contribute to the movement of cells movement by gliding, swimming, twitch, or crawling (Wolgemuth 2011).
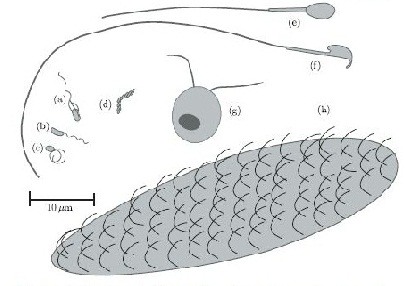
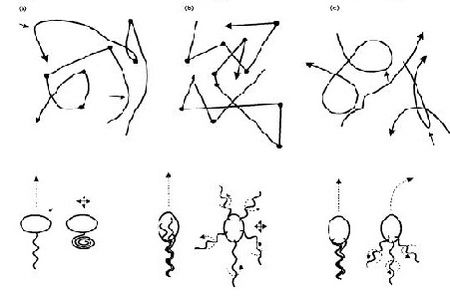
In terms of cell motility, an organism is defined as a “swimmer” if it moves by creating a periodic change in the shape of its body (Lauga and Powers 2008) (Figure 1). Bacteria and Archaebacteria use ionic flux channels to drive their molecular motors that power the motion of their filamentary objects (Wolgemuth 2011). For example, E. coli use flagella that rotate counterclockwise and form bundles in order to push the bacteria forward (Armitage and Schmittt 1997) (Figure 1a). When the bacteria switch to counterclockwise rotation the bundles are broken apart and the cell tumbles (Figure 2b); after the bundles reform the bacteria is facing a new direction in which it can move (Armitage and Schmitt 1997). Calobacter crescentus’ filaments turn a clock wise motion to pushes the bacterium forward, while counter-clockwise motion pulls the bacterium backward (Lauga and Powers 2008) (Figure 1b); Rhodobacter sphaeroides’ filaments only turn one direction (Lauga and Powers 2008) and periodically stop to re-orient itself (Armitage and Schmidt 1997) (Figure 1c and Figure 2a). In a similar manner, Sinorhizobium_meliloti, has several right-handed flagella that allow for quick forward swimming when the flagella form bundles and directional changes in which the flagella rotate at different rates (Figure 2c) (Armitage and Schmidt 1997). Other examples of bacteria with external flagella include sperm that use their flagella to produce a whip-like motion because its molecular motors are present throughout its filament (Figure 1e and 1f) (Lauga and Powers 2008). Furthermore, some bacteria do not need external flagella to move; Spiroplasma, doesn’t have flagella, but instead swims by circulating the kinks that are throughout its body (Figure 1d) (Lauga and Powers 2008).
Spirochetes are a phylum of bacteria that contain internal flagella (Lauga and Powers 2008) that are located within its periplasmic space that lies between the cell wall complex and the bacteria’s outer membrane (Dombrowski et al. 2009). In these bacteria, the flagella extend from each end of the spirochete, thus wrapping around the entire body of the bacteria (Lauga and Powers 2008); this gives the bacteria either a helical or flat wave shape depending in the species (Dombrowksi et al. 2009). Since flagella in spirochetes rotate within its periplasmic space a spirochetes flagella contain both skeletal and motile functions (Dombrowski et al 2009). The internal flagella allow spirochetes to quickly swim through viscous fluids that normally cause other species of bacteria to slow down; additionally, since their flagella are located internally spirochetes are protected from extreme environmental conditions and some antibiotics (Dombrowski et al. 2009).
Eukaryotes, on the other hand, have larger flagella cilia than bacteria (Lauga and Powers 2008) and these structures are powered by dynein motors that are located along the length of the filaments (Wolgemuth 2011). Additionally, other organisms have multiple flagella, such as Chlamydomonas reinhardtii, an algae that exhibits ciliary and flagellar beat patterns (Lauga and Powers 2008) and recent studies have shown that is uses a “run and tumble” swimming mechanism that is powered by the oscillations of its flagella (Wolgemuth 2011) (Figure 1g); Paramecium on the other hand uses the coordinated beat patterns of their cilia to move (Figure 1h).
New technological advances in the field microcopy have led an increase in the study and experimentation of cell motility. Brownian motion models are being replaced by more complex physical equations that have been derived to model avenues that range from bacterial turbulence, swarming dynamics and wound healing to Lyme disease.
Technological Advances
Light-microscopy has normally been used to observe and track cells as they are moving. Now, however, fluorescent dyes can be used to stain a bacterium’s flagella, thus illuminating the key cellular structures are required for a bacterium to swim (Lauga and Powers 2008). Additionally, a technique known as “optical trapping” uses a laser beam to generate a change in momentum in cells that results in generation of force (Koning et al. 1996); measuring this change in force allows for the recording of the interactions between molecules that contain single motor proteins (Nabiev et al. 2008). Atomic force microscopy, on the other hand, can directly measure the force generated by cilia (Lauga and Powers 2008).
Reynolds Number
The world of microscopic organisms involves fluids that are highly viscous in nature and dominate any inertial forces that may be present (Happel and Brenner 1991); therefore, given these conditions the physics that governs the movements of these organisms at a microscopic scale can be described by a low Reynolds Number (Lauga and Powers 2008). The Reynolds Number is a dimensionless quantity that is based on the Navier-Stokes Equation which describes the motion of an incompressible Newtonian fluid. The Reynolds number is the ratio of inertia to viscosity of a fluid (Wolgemuth 2008); therefore it allows for a qualitative description of the flow regime from the Navier-Stokes equation (Lauga and Powers 2008) (Table 1).
Biophysical Studies
Bacterial Turbulence
It is suspected that as the concentration of bacteria increases in a given area should lead to a decrease in the Reynolds number because increasing the concentration of bacteria, increases the fluid flow between neighboring bacteria will feel drag due to the velocity difference between each bacterium (Wolgemuth 2008). However, bacteria such as Bacillus subtilis, shows an increase in Reynolds number when there bacteria are found in dense colonies (Wolgemuth 2008). In these areas, a jet-like fluid motion is observed that has speeds which are faster than the speed of each bacterium; these jet-like motions are similar to fluid dynamics known as von Karman vortex street, in which the Reynolds is greater than fifty (Wolgemuth 2008). It is these swimming patterns which have high Reynolds numbers for their fluid dynamics that are known as “bacterial turbulence” (Wolgemuth 2008).
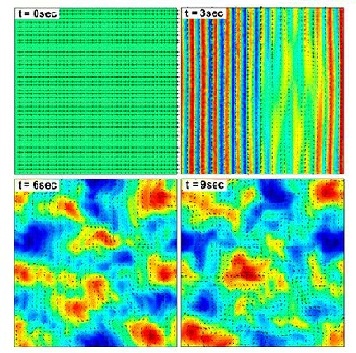
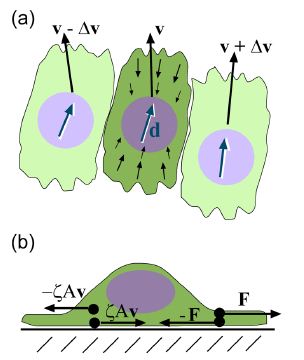
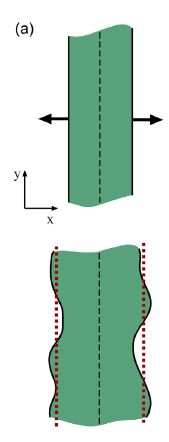
Wolgemuth (2008) developed a two-phase model that analyzed the group swimming dynamics of dense colonies of bacteria i.e. “bacterial turbulence.” Wolgemuth’s model treats the fluid and bacteria independently, and is based off of rod-like bacteria, like Bacillus subtilis, in which entropic forces will favor the restricted alignment of the bacteria (Wolgemuth 2008) (Figure 3). Wolgemuth (2008) defined a series of equations and parameters that make up his two-phase group swimming model; these parameters reproduce the behavior that is observed by in regions that “bacterial turbulence” are present (Figure 4 and 5).
Understanding the behavior associated with “bacterial turbulence” has industrial and medical applications. Large concentrations of bacteria are found in filtration systems, like dead-end filtration (see wiki), in which water containing bacteria forced through a microfilter (Wolgemuth 2008). Additionally, biofilmsare produced by an aggregation of bacteria to a single area and are known to cause infections and corrosion (Wolgeumuth 2008).
Swarming Dynamics
While the biofilms can be formed by aggregation of bacteria, bacterial swarming also contributes the formation of biofilm communities. These pathogenic bacteria form biofilms within the human body during transplant procedure, for example, Proteus mirabilis swarm to form biofilms on urinary catheters which can causes blockages in the catheters and lead to pyelonephritis, septicemia and shock (Sharma and Anand 2002). Bacterial swarming can also produce virulent proteins that can cause kidney infections, wound infections, and possibly cystic fibrosis (Sharma and Anand 2002).
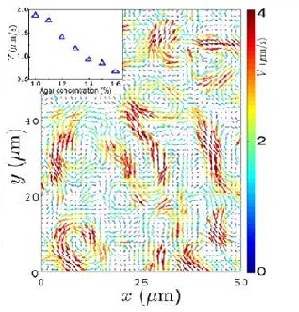
Zhang et al. (2009) studied swarming motion of Paenibacillus dendritiformis colonies on semi-solid agar plates (Figure 6). The scientists were able to measure the speeds of each bacterium and the velocity fields that occur within the bacteria. This allowed them to observe the relationship between the bacteria’s average speed and the length and time scales of the jets that are characteristic of the swarming motion (Zhang et al. 2009) (Figure 6). Add more here..
Wound Healing
Epithelial cells have been observed to crawl in order to heal a wound; this crawling powered by the cell’s actin cytoskeleton (Lee and Wolgemuth 2011). The general process is a three step process, that first requires that the actin located in the front of the cells needs to be polymerized, the organism needs to obtain some kind of grip to its surrounding environment, and finally enough force needs to be generated to move the rest of the cell forward (Wolgemuth 2011). Lee and Wolgemuth (2011) studied the possibility that the cellular movement that occurs during wound healing is a mechanical process that is based on cells crawling and not powered by myosin or other biochemical proteins. The scientists developed a model to incorporate the characteristics of single migrating cells and cell-cell adhesions. Their model illustrated that the cells are aligned along a set direction and velocity, and a difference in velocity between neighboring cells can cause viscous stress that produces torque and therefore causes rotational movement between the neighboring cells (Figure 7a). Additionally, based on Newton’s third law of motion, they assumed that a cell which exerts a force on a substrate will experience an equal and opposite force exerted onto it from the substrate. This causes the cell to generate a thrust force that is counteracted by a drag force exerted by the substrate. The result is the production of dipole stress in the cell (Figure 7b).
Lee and Wolgemuth (2011) first applied their model to examine the healing process in a one-dimensional wound. In these wounds, a straight cut is made through the layer of cells and the rate at which the cells fill this area was measured. The dipole stress in this case causes pressure to exert a compressive force into the wounded area; this causes an expansive pressure to be exerted back onto the cell strip. It is this pressure that causes cells to spread over the wounded area (Figure 8) (Lee and Wolgemuth 2011).
Lee and Wolgemuth (2011) also illustrated the complex movements that cells undergo when healing two-dimensional wounds. In the case, the force distribution among the cell-filled area causes instabilities that lead to the observation of vortices, jets and fingering-like appearance in the movement of the cells (Figure 9).
Lyme Disease
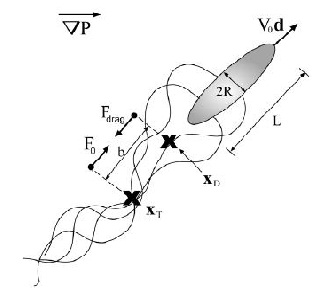
Lyme disease is caused by the spirochete,Borrelia burgdorferi, which is found in ticks that have a mutualistic relationship with the bacteria. The ticks obtain the bacteria when they bite mice or deer that are infected with Lyme disease. The disease is then transmitted to humans through a bite from an infected tick PubMed: Lyme disease (Diagram 1). Studies with Borrelia burgodferi have discovered have discovered a relationship between the bacteria’s motility and its virulence (Dombrowski et al 2009). These spirochetes have flat-wave morphologies, and it has been found that these bacteria are able to swim due to the thrust generated by the deformation of its cell wall that it caused by the rotation of its periplasmic flagella (Dombrowski et al. 2009) (Figure 12). This deformation of the cell wall generates a force back that causes the periplasmic flagella to also deform (Dombrowski). In order to test whether this qualitative mechanism is sufficient to cause the flat-wave morphology observed in Borrelia burgdorferi, Dombrowski et al. (2009) developed a mathematical model in which they characterized the periplasmic flagella and cell wall of the bacteria as elastic objects (Figure 13).
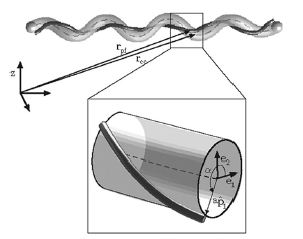
Model of Borrelia burgdorderi
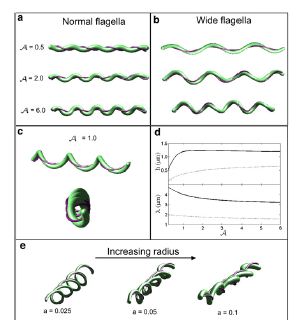
Dombrowski et al. (2009) assumed that the flagella of the bacteria are contained to a single position on the outer perimeter of the bacteria’s cell wall, and that the flagella are free to slide. The scientists found that when the cell wall is more rigid than the flagella than the bacteria is almost straight with its flagella wrapping around the cell wall. Furthermore, increasing the ratio of the bacteria’s ratio of twisting to bending the cell wall was observed to deform into the flat-wave morphology that is normally observed in Borrelia burgdorderi (Figure 13a and d) (Dombrowski et al. 2009). Additionally, the model predicted that in this flat-wave morphology the periplasmic flagella will wrap around the cell wall in the direction opposite in which it is located (Dombrowski et al. 2009). When the bacteria’s ratio of twisting to bending equal to 1.0 the amplitude of the bacteria increases slightly but most remains constant, but its wavelength decreases; in this form the shape of the cell is not the normally observed flat-wave morphology, but a flattened helical form (Figure 13c) (Dombrowski et al. 2009). Finally, it was observed that increasing the cell’s radius led the cell to morph from a more helical shape to flattened (Figure 13e). Overall, the scientist’s model illustrated that the flat-wave morphology observed in Borrelia burgdorferi is indeed created by the coupling of the helical periplasmic flagella to the cell wall.
Future Directions
Desinging articial swimminger with low reynolds numbers. optimization hydrodynamic interactions biological locomtion in complex fluids
Conclusions
Wolgemuth trends paper, the whole point of using math and physics and creating models is the applications of the model after they are created..