Suppression of Peptidoglycan Remodeling: Difference between revisions
| (27 intermediate revisions by the same user not shown) | |||
| Line 15: | Line 15: | ||
==Structure and Function== | ==Structure and Function== | ||
<br> The peptidoglycan layer is located in the bacterial cell wall, consisting of chains of two alternating amino sugars, N-acetylglucosamine (an amide derivative of the monosaccharide glucose) and N-acetylmuramic acid (a combination of N-acetylglucosamine and phosphoenolpyruvate). The alternating amino sugars are linked by Teichoic acids, which are chains of phosphodiester-linked glycerol or ribitol.<ref name=slon/> Parallel chains of amino sugars can also be connected by cross-bridges made of extensions of peptides to form tetrapeptides, with m-Diaminopimelic acid binding D-Alanine.<ref>[https://open.oregonstate.education/generalmicrobiology/chapter/bacteria-cell-walls/] Bruslind, Linda. n.d. “Bacteria: Cell Walls.” in <i>General Microbiology.<i/> Oregon State University.</ref> | <br> The peptidoglycan layer is located in the bacterial cell wall, consisting of chains of two alternating amino sugars, N-acetylglucosamine (an amide derivative of the monosaccharide glucose) and N-acetylmuramic acid (a combination of N-acetylglucosamine and phosphoenolpyruvate).The alternating amino sugars are linked by Teichoic acids, which are chains of phosphodiester-linked glycerol or ribitol.<ref name=slon/> Parallel chains of amino sugars can also be connected by cross-bridges made of extensions of peptides to form tetrapeptides, with m-Diaminopimelic acid binding D-Alanine.<ref>[https://open.oregonstate.education/generalmicrobiology/chapter/bacteria-cell-walls/] Bruslind, Linda. n.d. “Bacteria: Cell Walls.” in <i>General Microbiology.<i/> Oregon State University.</ref> | ||
[[Image:Peptidoglycan.png|thumb|500px|right|Structure of Peptidoglycan.By Linda Bruslind. [https://open.oregonstate.education/generalmicrobiology/chapter/bacteria-cell-walls/].]] | [[Image:Peptidoglycan.png|thumb|500px|right|Structure of Peptidoglycan.By Linda Bruslind. [https://open.oregonstate.education/generalmicrobiology/chapter/bacteria-cell-walls/].]] | ||
[[Image:Sacculi.png|thumb|400px| | [[Image:Sacculi.png|thumb|400px|right|Electron Microscopy of Purified Sacculi. [https://pubmed.ncbi.nlm.nih.gov/18194336/].]] | ||
Peptidoglycan sacculi cross-linked by peptides form a closed, sac-shaped structure that surrounds the cytoplasmic membrane. Peptidoglycan sacculi have been purified from Escherichia coli by incubation with boiling 4% sodium dodecyl sulfate.<ref>[https://pubmed.ncbi.nlm.nih.gov/18194336/] Vollmer, Waldemar, Didier Blanot, and Miguel A. de Pedro. 2008. “Peptidoglycan Structure and Architecture.” <i>FEMS Microbiology Reviews<i/> 32(2):149–67. doi: 10.1111/j.1574-6976.2007.00094.x.</ref> While a bacterial cell contains a significant number of different kinds of molecules, there is only one peptidoglycan molecule in each bacterial cell, which contributes to 0.8% of the mass of the whole cell in Gram-negative bacteria.<ref name=slon/> | |||
The content of peptidoglycan sacculi could be different among bacterial species. In Gram-positive bacteria, such as Staphylococcus aureus, the tetrapeptide cross-bridges are made of L-alanine, D-glutamine, L-lysine, and D-alanine. In Gram-negative bacteria, on the other hand, the cross-bridges are constituted of L-alanine, D-glutamic acid, m-diaminopimelic acid, and D-alanine. Gram-positive bacteria typically have many layers (3-20) of peptidoglycan chains outside the cytoplasmic membrane, whereas Gram-negative bacteria often have one or two layers of peptidoglycan between the inner and outer membrane.<ref name=slon/> | The content of peptidoglycan sacculi could be different among bacterial species. In Gram-positive bacteria, such as Staphylococcus aureus, the tetrapeptide cross-bridges are made of L-alanine, D-glutamine, L-lysine, and D-alanine. In Gram-negative bacteria, on the other hand, the cross-bridges are constituted of L-alanine, D-glutamic acid, m-diaminopimelic acid, and D-alanine. Gram-positive bacteria typically have many layers (3-20) of peptidoglycan chains outside the cytoplasmic membrane, whereas Gram-negative bacteria often have one or two layers of peptidoglycan between the inner and outer membrane.<ref name=slon/> | ||
Peptidoglycan plays a crucial role in the survival and reproduction of bacteria. It is the main component of the bacterial cell wall, forming a strong net-like structure that maintains the shape of the cell. Since bacteria are unicellular organisms, it is extremely important to protect the only cell from the outside environment. When the bacteria experience a significant osmotic pressure difference across the cell membrane, the cell envelope could prevent the cell from shrinking or expanding too much so that it lyses and dies.<ref>[https://www.sciencedirect.com/science/article/abs/pii/S0740002014001890] Al-Nabulsi, Anas A., Tareq M. Osaili, Reyad R. Shaker, Amin N. Olaimat, Ziad W. Jaradat, Noor A. Zain Elabedeen, and Richard A. Holley. 2015. “Effects of Osmotic Pressure, Acid, or Cold Stresses on Antibiotic Susceptibility of Listeria Monocytogenes.” <i>Food Microbiology<i/> 46:154–60. doi: 10.1016/j.fm.2014.07.015.</ref> | |||
Peptidoglycan plays a crucial role in the survival and reproduction of bacteria. It is the main component of the bacterial cell wall, forming a strong net-like structure that maintains the shape of the cell. Since bacteria are unicellular organisms, it is extremely important to protect the only cell from the outside environment. When the bacteria experience a significant osmotic pressure difference across the cell membrane, the cell envelope could prevent the cell from shrinking or expanding too much so that it lyses and dies.<ref name=osmo>[https://www.sciencedirect.com/science/article/abs/pii/S0740002014001890] Al-Nabulsi, Anas A., Tareq M. Osaili, Reyad R. Shaker, Amin N. Olaimat, Ziad W. Jaradat, Noor A. Zain Elabedeen, and Richard A. Holley. 2015. “Effects of Osmotic Pressure, Acid, or Cold Stresses on Antibiotic Susceptibility of Listeria Monocytogenes.” <i>Food Microbiology<i/> 46:154–60. doi: 10.1016/j.fm.2014.07.015.</ref> | |||
Peptidoglycan is also associated with binary fission, a reproductive process in which one bacterium divides into two bacteria. To successfully divide one cell into two, the peptidoglycan must grow as the bacterium elongates and quickly enclose both cells after division so that both of the progeny cells have complete cell envelopes.<ref>[https://biologydictionary.net/peptidoglycan/] Editors, B. D. 2017. “Peptidoglycan.” <i>Biology Dictionary.<i/> Retrieved April 8, 2021 (https://biologydictionary.net/peptidoglycan/).</ref> | Peptidoglycan is also associated with binary fission, a reproductive process in which one bacterium divides into two bacteria. To successfully divide one cell into two, the peptidoglycan must grow as the bacterium elongates and quickly enclose both cells after division so that both of the progeny cells have complete cell envelopes.<ref>[https://biologydictionary.net/peptidoglycan/] Editors, B. D. 2017. “Peptidoglycan.” <i>Biology Dictionary.<i/> Retrieved April 8, 2021 (https://biologydictionary.net/peptidoglycan/).</ref> | ||
<br> | |||
==Role in Staining Protocols== | |||
<br> | |||
Gram staining is the technique used to distinguish bacteria of two large groups: Gram-positive and Gram-negative. To distinguish Streptococcus pneumoniae from human lung cells, this technique was developed by the Danish bacteriologist Hans Christian Gram, where the name of this method came from.<ref name=stain> [https://doi.org/10.1002/9780471729259.mca03cs00. Coico, Richard. 2006. “Gram Staining.” <i>Current Protocols in Microbiology<i/> 00(1):A.3C.1-A.3C.2. doi: https://doi.org/10.1002/9780471729259.mca03cs00.]</ref> Peptidoglycan in Gram-positive bacterial cell wall is able to retain the crystal violet‐iodine complex and the safranin counterstain after treated with alcohol, turning into purple. Peptidoglycan in Gram-negative bacterial cell wall, on the other hand, appears pink after treated with those complex.<ref name=stain/> | |||
Gram-positive bacteria typically have single membrane surrounded by thick layers of peptidoglycan chains, which contribute to 50–90% of cell envelope. This mesh-like structure is able to retain enough crystal violet in the stain complex to color the cell purple. Firmicutes and Actinobacteria bacteria usually show positive results after treated with gram stain complex.<ref>[https://https://archive.org/details/brockbiologyofmi00madi] Madigan, Michael T., John M. Martinko, and Jack Parker. 2003. <i>Brock Biology of Microorganisms.<i/> Upper Saddle River, NJ : Prentice Hall/Pearson Education.</ref> | |||
Gram-negative bacteria often have a thin layer of peptidoglycan between the inner and outer cellular membrane. Proteobacteria and Bacteroidetes, which are two phyla of gut bacteria for digesting food, are usually stained Gram-negative.<ref name = slon/> | |||
<br> | <br> | ||
==Biosynthesis== | ==Biosynthesis== | ||
<br>First, glutamine would transfer an amino group to fructose 6-phosphate, producing glucosamine-6-phosphate. Then, acetyl CoA would donate an acetyl group to the amino group on fructose 6-phosphate to make N-acetyl-glucosamine-6-phosphate, which would then turn into N-acetyl-glucosamine-1-phosphate, a monophosphate. After the reaction between N-acetyl-glucosamine-1-phosphate and Uridine triphosphate, an inorganic pyrophosphate is substituted with N-acetyl-glucosamine-1-phosphate, producing UDP-N-acetylglucosamine.<ref name=synth> White, D. (2007). <i>The physiology and biochemistry of prokaryotes<i/> (3rd ed.). NY: Oxford University Press Inc.</ref> | |||
Following the creation of the precursor for the N-acetylglucosamine in peptidoglycan, a lactyl group would be added to the glucosamine which converts UDP-N-acetylglucosamine into UDP-N-acetylmuramic acid. A phosphate from the alpha carbon of phosphoenolpyruvate would also be given off by the C3 hydroxyl group, creating an enol derivative that would later be reduced by NADPH. By adding five amino acids including D-alanyl-D-alanine, UDP-N-acetylmuramic acid can turn into a pentapeptide, completing the process of producing a precursor for N-acetylmuramic acid.<ref name=synth/> | |||
In the cytoplasmic membrane, a lipid carrier named bactoprenol carries peptidoglycan precursors across the cell membrane. The mechanism behind this transport remains elusive, but precursors would be added to peptidoglycan once they get out of the cell membrane.<ref name=synth/> | |||
<br> | <br> | ||
== | |||
==Antibiotics that Break Down Peptidoglycan== | |||
[[Image:VISA.png|thumb|300px|right| A vancomycin-intermediate <i>Staphylococcus aureus</i> strain isolated from the patient after failed vancomycin therapy.[https://remote.kenyon.edu/pmc/articles/PMC2806658/,DanaInfo=www.ncbi.nlm.nih.gov,SSL+?tool=pmcentrez&report=abstract].]] | [[Image:VISA.png|thumb|300px|right| A vancomycin-intermediate <i>Staphylococcus aureus</i> strain isolated from the patient after failed vancomycin therapy.[https://remote.kenyon.edu/pmc/articles/PMC2806658/,DanaInfo=www.ncbi.nlm.nih.gov,SSL+?tool=pmcentrez&report=abstract].]] | ||
Peptidoglycan is unique to bacteria, which serves as a great target for antibiotics. | |||
Penicillin, a famous antibiotic widely used around the world, targets the transpeptidase that cross-links the peptides.<ref name=slon/>Penicillin kills bacteria by inhibiting the biosynthesis of peptidoglycans, specifically cause the dysfunction of penicillin-bind proteins that catalyze the formation of tetrapeptide cross-bridges, weakening the cell wall. Since the peptidoglycans are no longer able to maintain the proper osmotic pressure, too much water would flow into the cell and result in cell lysis.<ref name=osmo/>Moreover, given that penicillin interferes with the final step in peptidoglycan formation, excessive peptidoglycan precursors would build up in the cell, activating bacterial cell wall hydrolases and autolysins to break down the existing peptidoglycans.<ref> [https://go.drugbank.com/drugs/DB01053] “Benzylpenicillin.” Retrieved April 8, 2021.</ref> | |||
Vancomycin is another antibiotic that targets the formation of peptidoglycans in Gram-positive bacteria. Under normal conditions, D-Alanine would bind to m-Diaminopimelic acid to form a cross-bridge between parallel chains of peptidoglycans. However, vancomycin is able to bind to D-Ala-D-Ala, blocking the formation of cross-bridge. Despite the antibiotics available to fight against bacteria by targeting peptidoglycan biosynthesis, some bacteria can combine with antibiotics, which has been a growing problem for the world. A study showed the existence of a vancomycin-intermediate Staphylococcus aureus, a strain that is difficult to detect. This vancomycin-intermediate Staphylococcus aureus could make the treatment of vancomycin ineffective.<ref>[https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2806658/] Howden, Benjamin P., John K. Davies, Paul D. R. Johnson, Timothy P. Stinear, and M. Lindsay Grayson. 2010. “Reduced Vancomycin Susceptibility in Staphylococcus Aureus, Including Vancomycin-Intermediate and Heterogeneous Vancomycin-Intermediate Strains: Resistance Mechanisms, Laboratory Detection, and Clinical Implications.” <i>Clinical Microbiology Reviews<i/> 23(1):99–139. doi: 10.1128/CMR.00042-09.</ref> | |||
<br> | |||
==Automatic Degradation== | |||
<br> | |||
Bacteria employ several methods of degradation of peptidoglycan with the purpose of assembly and disassembly of the bacterial envelope during growth and division. Enzymes that hydrolyze the peptidoglycan of the enzyme-producing organisms are called autolysins.<ref>[https://https://www.ncbi.nlm.nih.gov/pmc/articles/PMC2659621/] Humann, Jessica, and Laurel L. Lenz. 2009. “Bacterial Peptidoglycan-Degrading Enzymes and Their Impact on Host Muropeptide Detection.” <i>Journal of Innate Immunity<i/> 1(2):88–97. doi: 10.1159/000181181.</ref> These enzymes target the glycosidic bonds and the teichoic acids that cross-link the peptides of the peptidoglycan matrix, forming mesh-like structures.<ref>[https://pubmed.ncbi.nlm.nih.gov/24692449/]Atilano, Magda Luciana, Pedro Matos Pereira, Filipa Vaz, Maria João Catalão, Patricia Reed, Inês Ramos Grilo, Rita Gonçalves Sobral, Petros Ligoxygakis, Mariana Gomes Pinho, and Sérgio Raposo Filipe. 2014. “Bacterial Autolysins Trim Cell Surface Peptidoglycan to Prevent Detection by the Drosophila Innate Immune System.” <i>ELife<i/> 3:e02277. doi: 10.7554/eLife.02277.</ref> During the biosynthesis of peptidoglycan, autolysins break peptidoglycans in small sections in order for new units to form.<ref name=auto>[http://www.ncbi.nlm.nih.gov/pubmed/30169125]Clarke, Anthony J. 2018. “The ‘Hole’ Story of Predatory Outer-Membrane Vesicles.” <i>Canadian Journal of Microbiology<i/> 64(9):589–99. doi: 10.1139/cjm-2017-0466.</ref> The old peptidoglycan is broken down and replaced by the newly formed peptidoglycan for growth and elongation, a process known as wall turnover.<ref>[http://www.ncbi.nlm.nih.gov/pubmed/10708363]Smith, Thomas J., Steve A. Blackman, and Simon J. Foster. 2000. “Autolysins of Bacillus Subtilis: Multiple Enzymes with Multiple Functions.” <i>Microbiology (Reading, England)<i/> 146 ( Pt 2):249–62. doi: 10.1099/00221287-146-2-249.</ref> During this process, autolysins hydrolyze the β-(1,4) glycosidic bond of the peptidoglycan and the linkage between N-acetylmuramoyl residues and L-amino acid residues.<ref name=auto/> | |||
These enzymes are found in all bacteria that obtain peptidoglycan and can lead to abnormal lysis when out of control.<ref>[https://pubmed.ncbi.nlm.nih.gov/28006655/]Haghighat, Setareh, Seyed Davar Siadat, Seyed Mehdi Rezayat Sorkhabadi, Abbas Akhavan Sepahi, and Mehdi Mahdavi. 2017. “Cloning, Expression and Purification of Autolysin from Methicillin-Resistant Staphylococcus Aureus: Potency and Challenge Study in Balb/c Mice.” <i>Molecular Immunology<i/> 82:10–18. doi: 10.1016/j.molimm.2016.12.013.</ref> When there are excessive autolysins in the bacterial cell, they would degrade the peptidoglycan matrix. Without the protection of the peptidoglycan cell wall, water from the outer environment would rush into the cell, causing overwhelming osmotic pressure across the membrane that ultimately leads to the bursting of the cell. | |||
<br> | <br> | ||
== | ==Antibiotics that Suppress Lysis of Peptidoglycan== | ||
[[Image: Complestatin and corbomycin.png|thumb|300px|right| Bacteria treated with corbomycin or complestatin shows a twisted phenotype and failed to divide into progeny cells.[https://www-nature-com.libproxy.kenyon.edu/articles/s41586-020-1990-9].]] | [[Image: Complestatin and corbomycin.png|thumb|300px|right| Bacteria treated with corbomycin or complestatin shows a twisted phenotype and failed to divide into progeny cells.[https://www-nature-com.libproxy.kenyon.edu/articles/s41586-020-1990-9].]] | ||
While antibiotics like penicillin and vancomycin inhibit the biosynthesis of peptidoglycans, other antibiotics have adopted a completely different method against bacteria. Researchers have found that complestatin and corbomycin block the action of autolysins, peptidoglycan hydrolases that are essential for remodeling the cell wall during growth. At the end of cell division, the two daughter cells need to separate into two identical cells, requiring the breakdown of peptidoglycan by autolysins. When this enzyme is inactivated, the cells fail to divide and thus disrupts the metabolism of the cell envelope.<ref name=antiremo/> | |||
<br> | |||
==Conclusion== | ==Conclusion== | ||
Antibiotic resistance has been a challenge for healthcare professionals for decades since the resistant strains outnumber the newly discovered antibiotics. Traditional antibiotics like penicillin and vancomycin defeat the bacteria by breaking the mesh-like peptidoglycan to cause overwhelming turgor pressure and lysis of the cell. However, with the widespread use of such antibiotics, bacteria have developed mechanisms to protect themselves from the binding of these antibiotics. Surprisingly, the opposite of breaking peptidoglycan: inactivation of autolysin by complestatin and corbomycin, which leads to the strengthening of peptidoglycan chains, also serve as a method to control bacterial growth. These findings give insight into the discovery and design of new antibiotics: there are two opposite directions in which researchers could expose bacteria to extreme conditions for the same process. | |||
<br> | |||
==References== | ==References== | ||
<references /> | <references /> | ||
<br><br>Authored for BIOL 238 Microbiology, taught by [mailto:slonczewski@kenyon.edu Joan Slonczewski], 2021, [http://www.kenyon.edu/index.xml Kenyon College]. | <br><br>Authored for BIOL 238 Microbiology, taught by [mailto:slonczewski@kenyon.edu Joan Slonczewski], 2021, [http://www.kenyon.edu/index.xml Kenyon College]. | ||
Latest revision as of 03:41, 17 April 2021
By [Frank Zhao]
Introduction
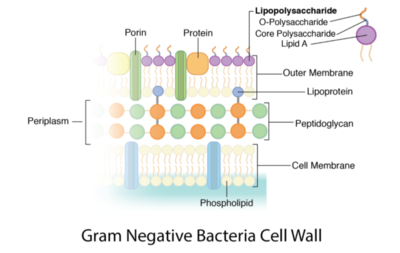
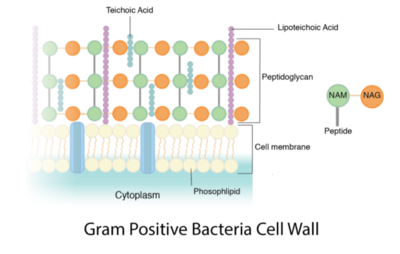
Peptidoglycan is a polymer made of sugars and amino acids that forms a layer outside the plasma membrane of bacterial cells. Peptidoglycans are cross-linked by peptides, serving as the cell wall that protects bacteria from the environment. Peptidoglycan limits the volume of the cell and thus it generates turgor pressure as the water rushes into the cell.[1] Gram-positive bacteria obtain a thicker peptidoglycan layer than Gram-negative bacteria but this layer is crucial to the survival of both types of bacteria.[2]
Many antibiotics target this component to kill the bacteria. For example, penicillin binds to penicillin-binding proteins and inhibits the synthesis of peptidoglycan, weakening the cell wall of bacteria. It has been discovered that a new mechanism could be used by antibiotics on peptidoglycan— blocking the action of autolysins, a peptidoglycan hydrolase that is essential for remodeling the bacterial cell wall during growth.[3] Studying how this new mechanism works could give us insight into developing new antibiotics against resistant strains.
Structure and Function
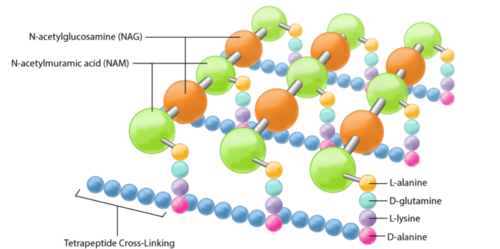
The peptidoglycan layer is located in the bacterial cell wall, consisting of chains of two alternating amino sugars, N-acetylglucosamine (an amide derivative of the monosaccharide glucose) and N-acetylmuramic acid (a combination of N-acetylglucosamine and phosphoenolpyruvate).The alternating amino sugars are linked by Teichoic acids, which are chains of phosphodiester-linked glycerol or ribitol.[1] Parallel chains of amino sugars can also be connected by cross-bridges made of extensions of peptides to form tetrapeptides, with m-Diaminopimelic acid binding D-Alanine.[4]
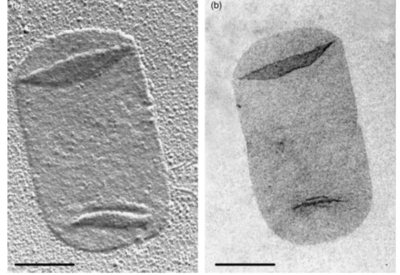
Peptidoglycan sacculi cross-linked by peptides form a closed, sac-shaped structure that surrounds the cytoplasmic membrane. Peptidoglycan sacculi have been purified from Escherichia coli by incubation with boiling 4% sodium dodecyl sulfate.[5] While a bacterial cell contains a significant number of different kinds of molecules, there is only one peptidoglycan molecule in each bacterial cell, which contributes to 0.8% of the mass of the whole cell in Gram-negative bacteria.[1]
The content of peptidoglycan sacculi could be different among bacterial species. In Gram-positive bacteria, such as Staphylococcus aureus, the tetrapeptide cross-bridges are made of L-alanine, D-glutamine, L-lysine, and D-alanine. In Gram-negative bacteria, on the other hand, the cross-bridges are constituted of L-alanine, D-glutamic acid, m-diaminopimelic acid, and D-alanine. Gram-positive bacteria typically have many layers (3-20) of peptidoglycan chains outside the cytoplasmic membrane, whereas Gram-negative bacteria often have one or two layers of peptidoglycan between the inner and outer membrane.[1]
Peptidoglycan plays a crucial role in the survival and reproduction of bacteria. It is the main component of the bacterial cell wall, forming a strong net-like structure that maintains the shape of the cell. Since bacteria are unicellular organisms, it is extremely important to protect the only cell from the outside environment. When the bacteria experience a significant osmotic pressure difference across the cell membrane, the cell envelope could prevent the cell from shrinking or expanding too much so that it lyses and dies.[6]
Peptidoglycan is also associated with binary fission, a reproductive process in which one bacterium divides into two bacteria. To successfully divide one cell into two, the peptidoglycan must grow as the bacterium elongates and quickly enclose both cells after division so that both of the progeny cells have complete cell envelopes.[7]
Role in Staining Protocols
Gram staining is the technique used to distinguish bacteria of two large groups: Gram-positive and Gram-negative. To distinguish Streptococcus pneumoniae from human lung cells, this technique was developed by the Danish bacteriologist Hans Christian Gram, where the name of this method came from.[8] Peptidoglycan in Gram-positive bacterial cell wall is able to retain the crystal violet‐iodine complex and the safranin counterstain after treated with alcohol, turning into purple. Peptidoglycan in Gram-negative bacterial cell wall, on the other hand, appears pink after treated with those complex.[8]
Gram-positive bacteria typically have single membrane surrounded by thick layers of peptidoglycan chains, which contribute to 50–90% of cell envelope. This mesh-like structure is able to retain enough crystal violet in the stain complex to color the cell purple. Firmicutes and Actinobacteria bacteria usually show positive results after treated with gram stain complex.[9]
Gram-negative bacteria often have a thin layer of peptidoglycan between the inner and outer cellular membrane. Proteobacteria and Bacteroidetes, which are two phyla of gut bacteria for digesting food, are usually stained Gram-negative.[1]
Biosynthesis
First, glutamine would transfer an amino group to fructose 6-phosphate, producing glucosamine-6-phosphate. Then, acetyl CoA would donate an acetyl group to the amino group on fructose 6-phosphate to make N-acetyl-glucosamine-6-phosphate, which would then turn into N-acetyl-glucosamine-1-phosphate, a monophosphate. After the reaction between N-acetyl-glucosamine-1-phosphate and Uridine triphosphate, an inorganic pyrophosphate is substituted with N-acetyl-glucosamine-1-phosphate, producing UDP-N-acetylglucosamine.[10]
Following the creation of the precursor for the N-acetylglucosamine in peptidoglycan, a lactyl group would be added to the glucosamine which converts UDP-N-acetylglucosamine into UDP-N-acetylmuramic acid. A phosphate from the alpha carbon of phosphoenolpyruvate would also be given off by the C3 hydroxyl group, creating an enol derivative that would later be reduced by NADPH. By adding five amino acids including D-alanyl-D-alanine, UDP-N-acetylmuramic acid can turn into a pentapeptide, completing the process of producing a precursor for N-acetylmuramic acid.[10]
In the cytoplasmic membrane, a lipid carrier named bactoprenol carries peptidoglycan precursors across the cell membrane. The mechanism behind this transport remains elusive, but precursors would be added to peptidoglycan once they get out of the cell membrane.[10]
Antibiotics that Break Down Peptidoglycan

Peptidoglycan is unique to bacteria, which serves as a great target for antibiotics.
Penicillin, a famous antibiotic widely used around the world, targets the transpeptidase that cross-links the peptides.[1]Penicillin kills bacteria by inhibiting the biosynthesis of peptidoglycans, specifically cause the dysfunction of penicillin-bind proteins that catalyze the formation of tetrapeptide cross-bridges, weakening the cell wall. Since the peptidoglycans are no longer able to maintain the proper osmotic pressure, too much water would flow into the cell and result in cell lysis.[6]Moreover, given that penicillin interferes with the final step in peptidoglycan formation, excessive peptidoglycan precursors would build up in the cell, activating bacterial cell wall hydrolases and autolysins to break down the existing peptidoglycans.[11]
Vancomycin is another antibiotic that targets the formation of peptidoglycans in Gram-positive bacteria. Under normal conditions, D-Alanine would bind to m-Diaminopimelic acid to form a cross-bridge between parallel chains of peptidoglycans. However, vancomycin is able to bind to D-Ala-D-Ala, blocking the formation of cross-bridge. Despite the antibiotics available to fight against bacteria by targeting peptidoglycan biosynthesis, some bacteria can combine with antibiotics, which has been a growing problem for the world. A study showed the existence of a vancomycin-intermediate Staphylococcus aureus, a strain that is difficult to detect. This vancomycin-intermediate Staphylococcus aureus could make the treatment of vancomycin ineffective.[12]
Automatic Degradation
Bacteria employ several methods of degradation of peptidoglycan with the purpose of assembly and disassembly of the bacterial envelope during growth and division. Enzymes that hydrolyze the peptidoglycan of the enzyme-producing organisms are called autolysins.[13] These enzymes target the glycosidic bonds and the teichoic acids that cross-link the peptides of the peptidoglycan matrix, forming mesh-like structures.[14] During the biosynthesis of peptidoglycan, autolysins break peptidoglycans in small sections in order for new units to form.[15] The old peptidoglycan is broken down and replaced by the newly formed peptidoglycan for growth and elongation, a process known as wall turnover.[16] During this process, autolysins hydrolyze the β-(1,4) glycosidic bond of the peptidoglycan and the linkage between N-acetylmuramoyl residues and L-amino acid residues.[15]
These enzymes are found in all bacteria that obtain peptidoglycan and can lead to abnormal lysis when out of control.[17] When there are excessive autolysins in the bacterial cell, they would degrade the peptidoglycan matrix. Without the protection of the peptidoglycan cell wall, water from the outer environment would rush into the cell, causing overwhelming osmotic pressure across the membrane that ultimately leads to the bursting of the cell.
Antibiotics that Suppress Lysis of Peptidoglycan
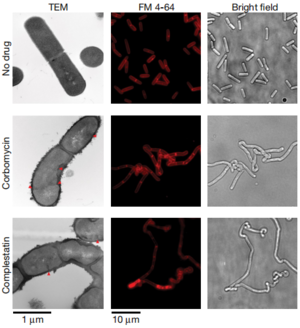
While antibiotics like penicillin and vancomycin inhibit the biosynthesis of peptidoglycans, other antibiotics have adopted a completely different method against bacteria. Researchers have found that complestatin and corbomycin block the action of autolysins, peptidoglycan hydrolases that are essential for remodeling the cell wall during growth. At the end of cell division, the two daughter cells need to separate into two identical cells, requiring the breakdown of peptidoglycan by autolysins. When this enzyme is inactivated, the cells fail to divide and thus disrupts the metabolism of the cell envelope.[3]
Conclusion
Antibiotic resistance has been a challenge for healthcare professionals for decades since the resistant strains outnumber the newly discovered antibiotics. Traditional antibiotics like penicillin and vancomycin defeat the bacteria by breaking the mesh-like peptidoglycan to cause overwhelming turgor pressure and lysis of the cell. However, with the widespread use of such antibiotics, bacteria have developed mechanisms to protect themselves from the binding of these antibiotics. Surprisingly, the opposite of breaking peptidoglycan: inactivation of autolysin by complestatin and corbomycin, which leads to the strengthening of peptidoglycan chains, also serve as a method to control bacterial growth. These findings give insight into the discovery and design of new antibiotics: there are two opposite directions in which researchers could expose bacteria to extreme conditions for the same process.
References
- ↑ 1.0 1.1 1.2 1.3 1.4 1.5 Slonczewski, J., and Foster J. W.. Microbiology: An Evolving Science. New York
- ↑ Anon. n.d. “Bacteria.” Basic Biology. Retrieved April 8, 2021
- ↑ 3.0 3.1 [1] Culp, Elizabeth J., Nicholas Waglechner, Wenliang Wang, Aline A. Fiebig-Comyn, Yen-Pang Hsu, Kalinka Koteva, David Sychantha, Brian K. Coombes, Michael S. Van Nieuwenhze, Yves V. Brun, and Gerard D. Wright. 2020. “Evolution-Guided Discovery of Antibiotics That Inhibit Peptidoglycan Remodelling.” Nature 578(7796):582–87. doi: 10.1038/s41586-020-1990-9.
- ↑ [2] Bruslind, Linda. n.d. “Bacteria: Cell Walls.” in General Microbiology. Oregon State University.
- ↑ [3] Vollmer, Waldemar, Didier Blanot, and Miguel A. de Pedro. 2008. “Peptidoglycan Structure and Architecture.” FEMS Microbiology Reviews 32(2):149–67. doi: 10.1111/j.1574-6976.2007.00094.x.
- ↑ 6.0 6.1 [4] Al-Nabulsi, Anas A., Tareq M. Osaili, Reyad R. Shaker, Amin N. Olaimat, Ziad W. Jaradat, Noor A. Zain Elabedeen, and Richard A. Holley. 2015. “Effects of Osmotic Pressure, Acid, or Cold Stresses on Antibiotic Susceptibility of Listeria Monocytogenes.” Food Microbiology 46:154–60. doi: 10.1016/j.fm.2014.07.015.
- ↑ [5] Editors, B. D. 2017. “Peptidoglycan.” Biology Dictionary. Retrieved April 8, 2021 (https://biologydictionary.net/peptidoglycan/).
- ↑ 8.0 8.1 Coico, Richard. 2006. “Gram Staining.” Current Protocols in Microbiology 00(1):A.3C.1-A.3C.2. doi: https://doi.org/10.1002/9780471729259.mca03cs00.
- ↑ [6] Madigan, Michael T., John M. Martinko, and Jack Parker. 2003. Brock Biology of Microorganisms. Upper Saddle River, NJ : Prentice Hall/Pearson Education.
- ↑ 10.0 10.1 10.2 White, D. (2007). The physiology and biochemistry of prokaryotes (3rd ed.). NY: Oxford University Press Inc.
- ↑ [7] “Benzylpenicillin.” Retrieved April 8, 2021.
- ↑ [8] Howden, Benjamin P., John K. Davies, Paul D. R. Johnson, Timothy P. Stinear, and M. Lindsay Grayson. 2010. “Reduced Vancomycin Susceptibility in Staphylococcus Aureus, Including Vancomycin-Intermediate and Heterogeneous Vancomycin-Intermediate Strains: Resistance Mechanisms, Laboratory Detection, and Clinical Implications.” Clinical Microbiology Reviews 23(1):99–139. doi: 10.1128/CMR.00042-09.
- ↑ [9] Humann, Jessica, and Laurel L. Lenz. 2009. “Bacterial Peptidoglycan-Degrading Enzymes and Their Impact on Host Muropeptide Detection.” Journal of Innate Immunity 1(2):88–97. doi: 10.1159/000181181.
- ↑ [10]Atilano, Magda Luciana, Pedro Matos Pereira, Filipa Vaz, Maria João Catalão, Patricia Reed, Inês Ramos Grilo, Rita Gonçalves Sobral, Petros Ligoxygakis, Mariana Gomes Pinho, and Sérgio Raposo Filipe. 2014. “Bacterial Autolysins Trim Cell Surface Peptidoglycan to Prevent Detection by the Drosophila Innate Immune System.” ELife 3:e02277. doi: 10.7554/eLife.02277.
- ↑ 15.0 15.1 [11]Clarke, Anthony J. 2018. “The ‘Hole’ Story of Predatory Outer-Membrane Vesicles.” Canadian Journal of Microbiology 64(9):589–99. doi: 10.1139/cjm-2017-0466.
- ↑ [12]Smith, Thomas J., Steve A. Blackman, and Simon J. Foster. 2000. “Autolysins of Bacillus Subtilis: Multiple Enzymes with Multiple Functions.” Microbiology (Reading, England) 146 ( Pt 2):249–62. doi: 10.1099/00221287-146-2-249.
- ↑ [13]Haghighat, Setareh, Seyed Davar Siadat, Seyed Mehdi Rezayat Sorkhabadi, Abbas Akhavan Sepahi, and Mehdi Mahdavi. 2017. “Cloning, Expression and Purification of Autolysin from Methicillin-Resistant Staphylococcus Aureus: Potency and Challenge Study in Balb/c Mice.” Molecular Immunology 82:10–18. doi: 10.1016/j.molimm.2016.12.013.
Authored for BIOL 238 Microbiology, taught by Joan Slonczewski, 2021, Kenyon College.
